Định lý cosin
Các hàm lượng giác cơ bản
Các hàm lượng giác cơ bản được xây dựng dựa trên mối quan hệ giữa các cạnh trong một tam giác vuông.
Sin (sin): Tỉ số giữa cạnh đối và cạnh huyền.
sin α = cạnh đối / cạnh huyền
Cosin (cos): Tỉ số giữa cạnh kề và cạnh huyền.
cos α = cạnh kề / cạnh huyền
Tang (tan): Tỉ số giữa cạnh đối và cạnh kề.
tan α = cạnh đối / cạnh kề
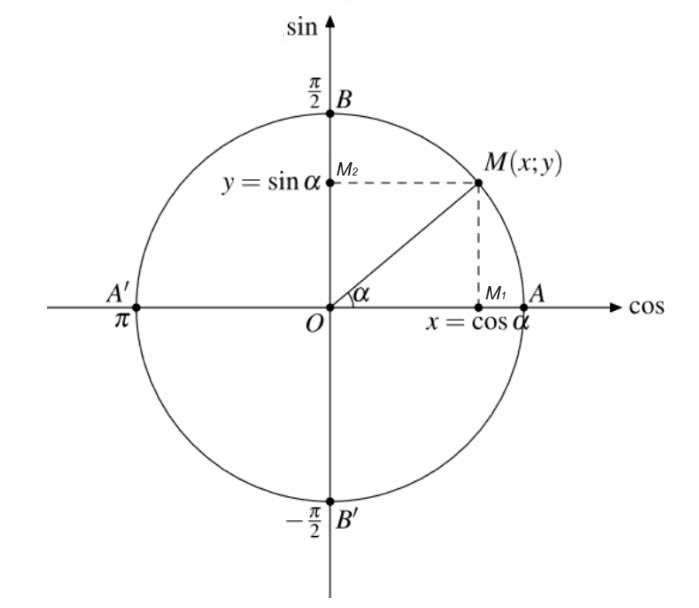
Đường tròn lượng giác
Đường tròn lượng giác là một công cụ trực quan giúp chúng ta hiểu rõ hơn về các hàm lượng giác. Nó là một đường tròn có bán kính bằng 1 đơn vị, chia thành 4 góc vuông. Mỗi điểm trên đường tròn tương ứng với một góc và các giá trị sin, cos của góc đó.
Lượng giácĐịnh lý cos và định lý sin là hai công cụ quan trọng trong lượng giác, giúp chúng ta giải quyết các bài toán liên quan đến tam giác. Chúng cho phép chúng ta tính toán các cạnh và góc của một tam giác khi biết một số thông tin nhất định.
Định lý cosin
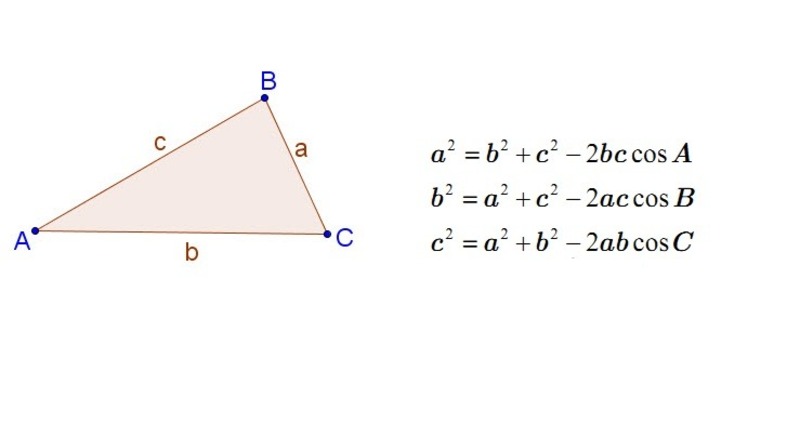
Nội dung: Trong một tam giác ABC bất kỳ, với a, b, c lần lượt là độ dài các cạnh đối diện với các góc A, B, C, ta có:
a² = b² + c² - 2bc.cosA
b² = a² + c² - 2ac.cosB
c² = a² + b² - 2ab.cosC
Ý nghĩa hình học
Định lý cos giúp ta liên hệ giữa độ dài các cạnh của một tam giác với góc đối diện của chúng. Nó đặc biệt hữu ích khi ta biết hai cạnh và góc xen giữa hoặc khi biết ba cạnh của tam giác.
Định lý sin
Nội dung: Trong một tam giác ABC bất kỳ, với a, b, c lần lượt là độ dài các cạnh đối diện với các góc A, B, C, và R là bán kính đường tròn ngoại tiếp tam giác, ta có:
a/sinA = b/sinB = c/sinC = 2R
Ý nghĩa hình học
Định lý sin cho ta mối liên hệ giữa các cạnh và các góc của một tam giác. Nó thường được sử dụng để giải các bài toán liên quan đến việc tính toán các góc hoặc cạnh còn thiếu của một tam giác khi biết một số thông tin nhất định.
Định lý cosĐịa lý và đo đạc
Xác định khoảng cách: Định lý cos giúp tính toán khoảng cách giữa các điểm trên mặt đất khi biết các góc và cạnh của tam giác hình thành bởi các điểm đó.
Vẽ bản đồ: Các nhà địa lý sử dụng định lý sin và cos để vẽ bản đồ, xác định vị trí các địa điểm.
Hệ thống định vị toàn cầu (GPS): Định lý sin và cos được sử dụng để tính toán khoảng cách giữa các vệ tinh và thiết bị thu nhận tín hiệu, từ đó xác định vị trí của thiết bị.
Kiến trúc và xây dựng
Tính toán kích thước: Định lý cos giúp tính toán các kích thước của các cấu trúc xây dựng như mái nhà, cầu thang, cột nhà.
Thiết kế nội thất: Ứng dụng để thiết kế các đồ nội thất có hình dạng đặc biệt.
Xây dựng các công trình lớn: Các kỹ sư sử dụng lượng giác để tính toán các thông số kỹ thuật của các công trình lớn như cầu cống, nhà cao tầng.
Hàng hải và hàng không
Xác định vị trí: Định lý sin và cos được sử dụng để xác định vị trí của tàu thuyền, máy bay.
Tính toán quãng đường: Tính toán quãng đường di chuyển của tàu thuyền, máy bay.
Điều hướng: Hỗ trợ việc điều hướng tàu thuyền, máy bay.
Vật lý
Cơ học: Tính toán lực, vận tốc, gia tốc trong các bài toán liên quan đến chuyển động.
Điện từ học: Tính toán các đại lượng điện từ như cường độ điện trường, cảm ứng từ.
Quang học: Tính toán đường đi của tia sáng.
Thiên văn học
Tính toán khoảng cách giữa các thiên thể: Định lý cos và sin được sử dụng để tính toán khoảng cách giữa các hành tinh, ngôi sao.
Xác định quỹ đạo của các hành tinh: Giúp các nhà thiên văn học hiểu rõ hơn về chuyển động của các thiên thể trong vũ trụ.
Ví dụ minh họa
Xác định chiều cao của một tòa nhà: Nếu biết khoảng cách từ chân tòa nhà đến một điểm quan sát và góc nâng từ điểm quan sát đến đỉnh tòa nhà, ta có thể sử dụng định lý tan để tính chiều cao tòa nhà.
Tính khoảng cách giữa hai điểm trên mặt đất: Nếu biết khoảng cách từ hai điểm đó đến một điểm thứ ba và góc tạo bởi hai đoạn thẳng nối hai điểm đó với điểm thứ ba, ta có thể sử dụng định lý cos để tính khoảng cách giữa hai điểm.

Lượng giácBài tập 1
Cho tam giác ABC có AB = 5cm, AC = 7cm và góc A = 60 độ. Tính độ dài cạnh BC và diện tích tam giác ABC.
Giải:
Tính BC: Áp dụng định lý cos: BC² = AB² + AC² - 2.AB.AC.cosA BC² = 5² + 7² - 2.5.7.cos60° BC² = 39 => BC ≈ 6.24 cm
Tính diện tích: S = (1/2).AB.AC.sinA = (1/2).5.7.sin60° ≈ 15.19 cm²
Bài tập 2
Một chiếc thang dài 5m dựa vào một bức tường tạo với mặt đất một góc 70 độ. Tính khoảng cách từ chân thang đến chân tường.
Giải:
Gọi x là khoảng cách từ chân thang đến chân tường.
Áp dụng định lý cos: 5² = x² + h² - 2.x.h.cos70° (Với h là chiều cao từ chân tường đến điểm thang chạm tường)
Tuy nhiên, trong bài toán này, chúng ta chỉ cần tính x. Sử dụng định lý sin: x/sin(90-70) = 5/sin90 => x = 5.sin20° ≈ 1.71 m
Bài tập 3
Một chiếc thuyền đi từ bến A đến bến B cách nhau 30km, xuôi dòng mất 2 giờ. Biết vận tốc của dòng nước là 2km/h. Tính vận tốc của thuyền so với nước đứng yên và góc giữa phương chuyển động của thuyền và bờ sông.
Giải:
Bài toán này liên quan đến vật lý hơn là lượng giác thuần túy, tuy nhiên ta vẫn có thể áp dụng định lý cos để giải.
... (Chi tiết giải sẽ hơi phức tạp, cần vẽ hình và phân tích lực)
Bài tập 4
Cho tam giác ABC có AB = 6cm, AC = 8cm và góc A = 60 độ. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Giải:
Áp dụng định lý sin: a/sinA = 2R => R = a/(2sinA) = 6/(2.sin60°) ≈ 3.46 cm
Trên đây là một số thông tin về định lý cos. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.